
How Does a Machine Learn?
Since the 2021 ChatGPT hype boom, everyone has heard about artificial intelligence, in computer science terms machine learning, and how unexpectedly it changed our daily lives. We encounter people who claim they have been using "AI" or they do the "AI" but what is it actually or is it as magical as it seems?
In this article, I'll explain what "AI" is, and how we can build a simple model—our own mini version of an "AI." I'll handle this subject from a computer scientist's point of view. So let's get started.
What is AI Really?
First of all the term AI or Artificial Intelligence is a wider subject than ChatGPT or the technologies like Large Language Models behind it. That same AI is used in Autonomous vehicles, heart disease detection, or even in investment banking. In computer science literature we call this fancy AI thing, Machine Learning. But is there real intelligence that tells a vehicle what to do or points to the disease at heart or can machines really learn?
The Truth About Machine Learning
How does your magical LLM produce an article that sounds like you? Or how do autonomous vehicles distinguish a traffic sign from another? The truth is that they don't know. The only thing they can do is make predictions. They predict your next word. They predict the sign they encounter is a speed limit. They predict the image you show them is a cat, but they have remarkably high accuracy with their predictions because they are trained for that task.
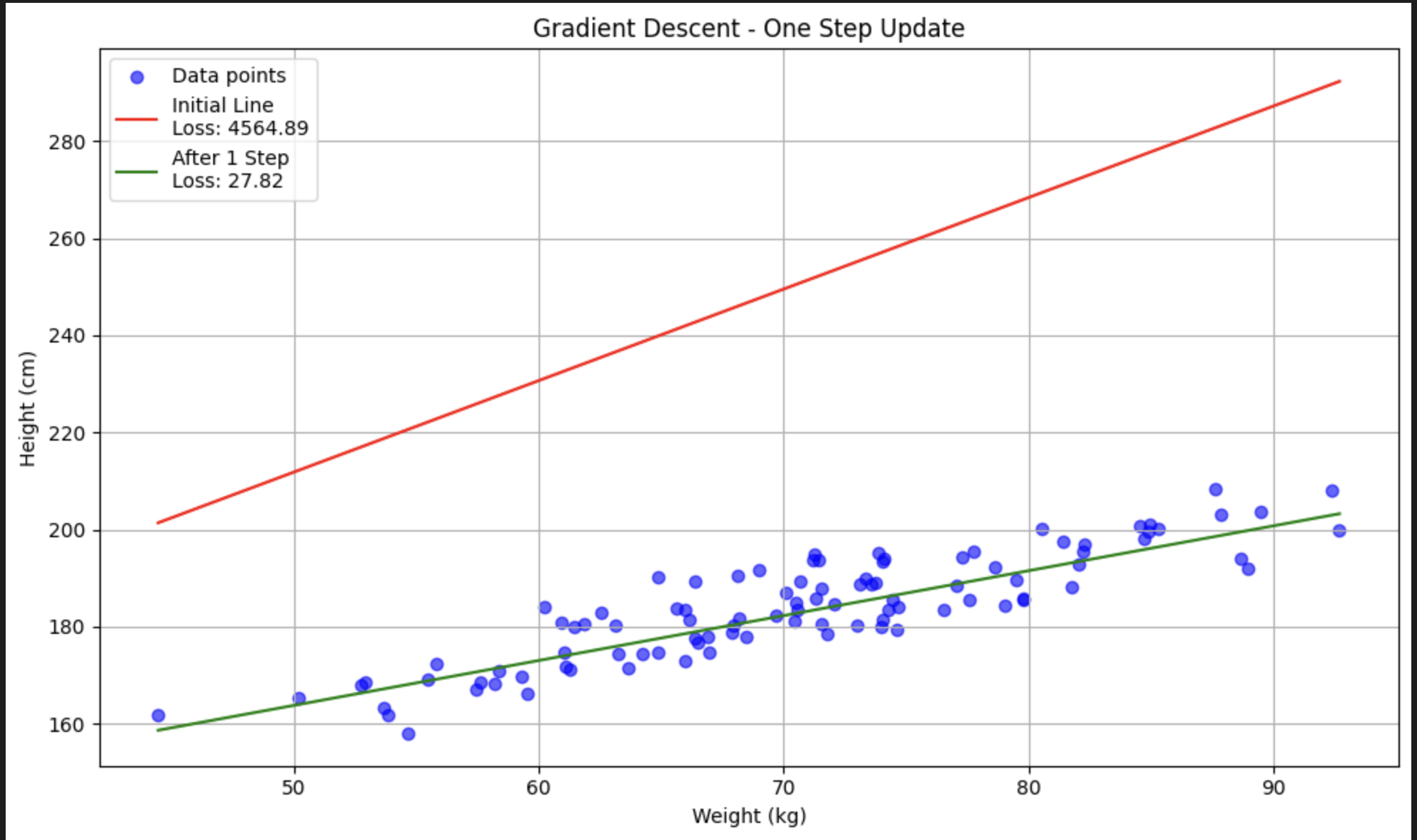
Linear Regression Example
Let's continue with a simple linear regression example. We want to predict the height of a person given their weight.
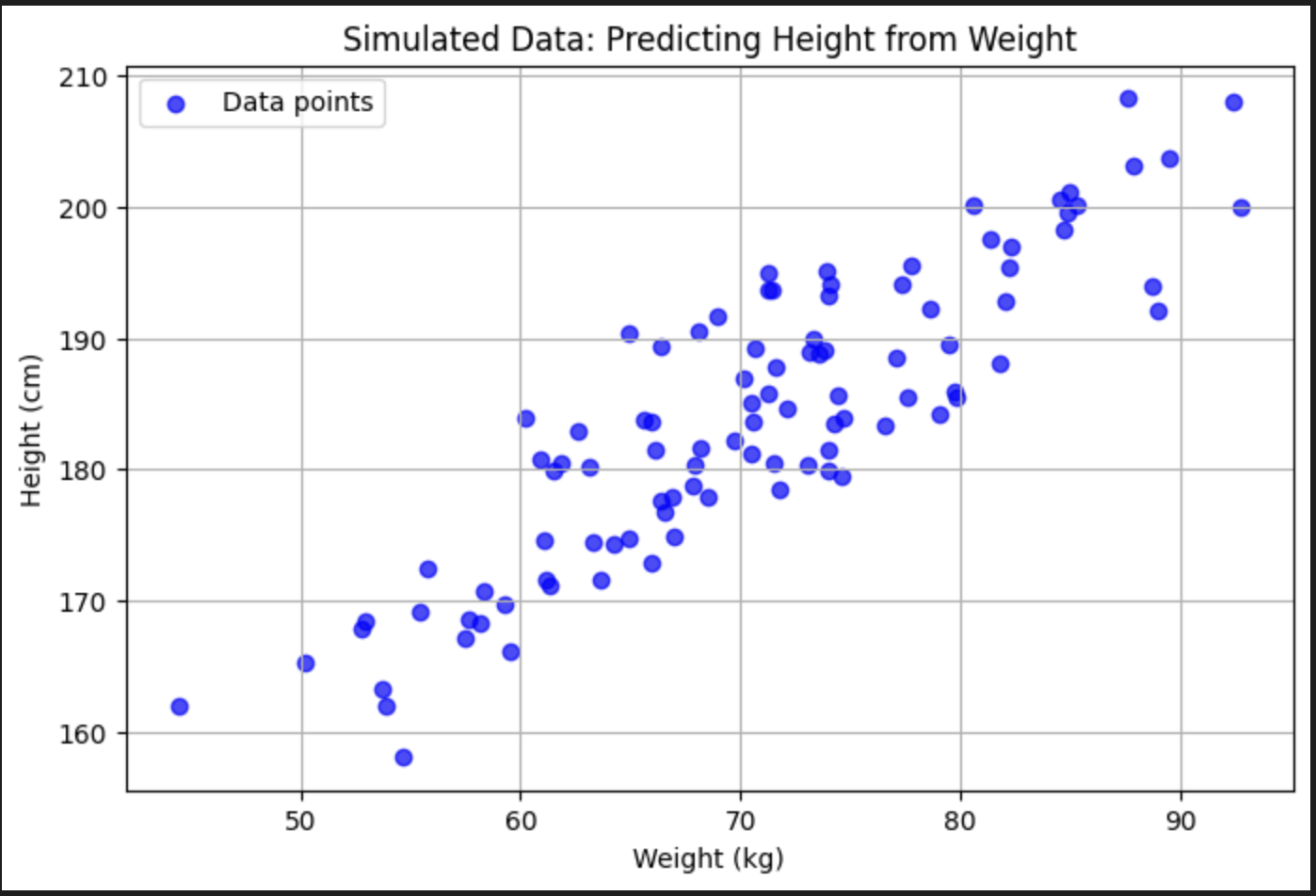
Our mission is to create a line, or a model, that can predict the actual value. For the initial state let's create a random line.
Predicted Height = (Slope * Weight) + Intercept
That might look familiar:
y = ax + b
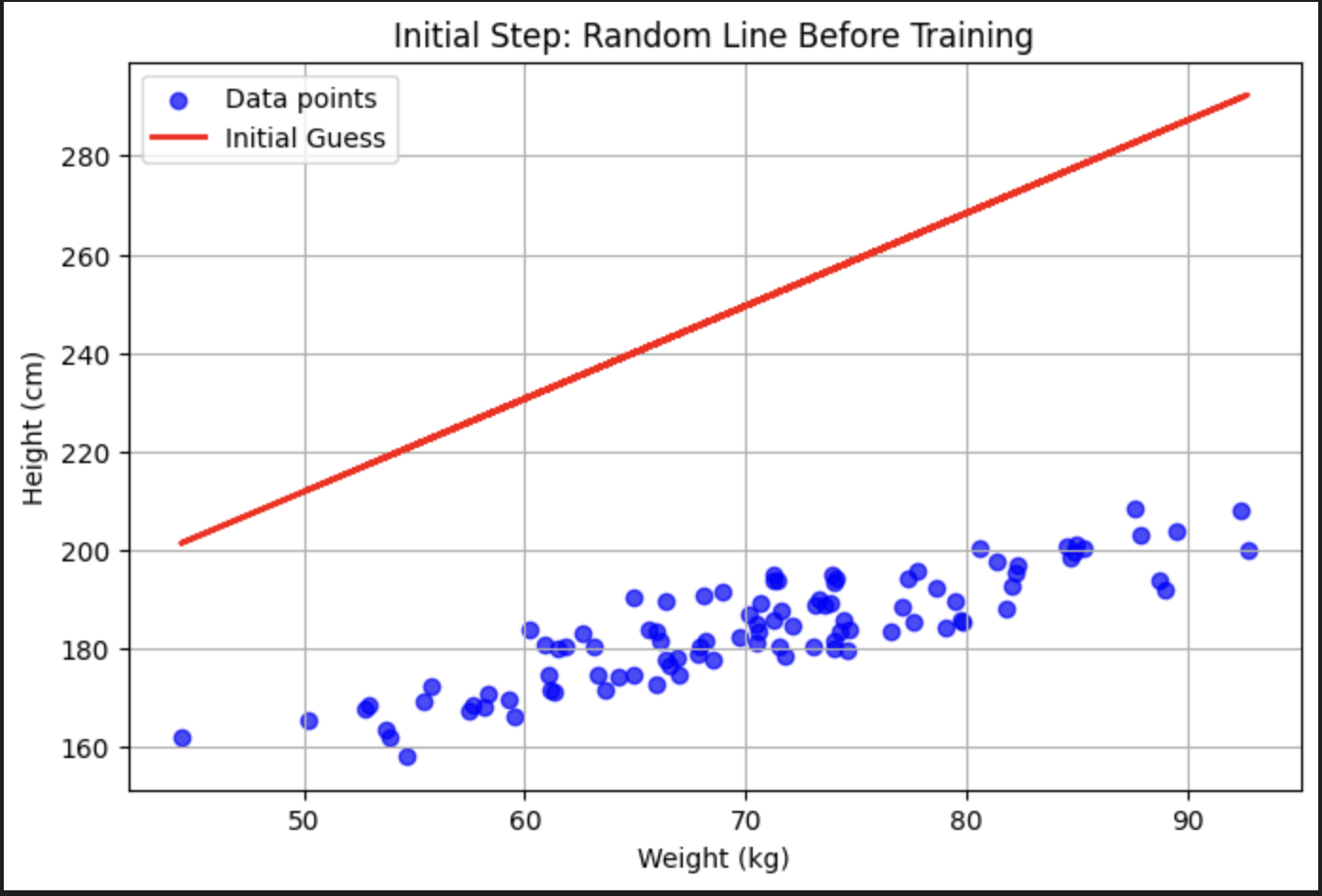
As you can see, even without having a former mathematical background, this line cannot even come close to the actual values. So we have to train that line to fit the actual values, but first, we have to know how bad our initial model was.
Loss Function
To quantify how "bad" our predictions are, we use a loss function. In linear regression, a common choice is the Mean Squared Error (MSE). It calculates the average of the squares of the differences between actual and predicted values.
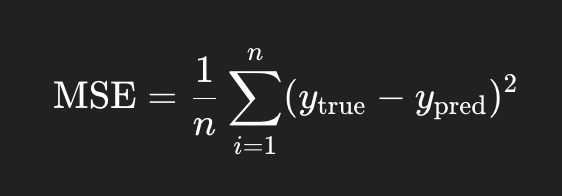
This gives us a single number representing how far off our model is. A high loss means our predictions are far from the real data. A low loss means we're doing well.
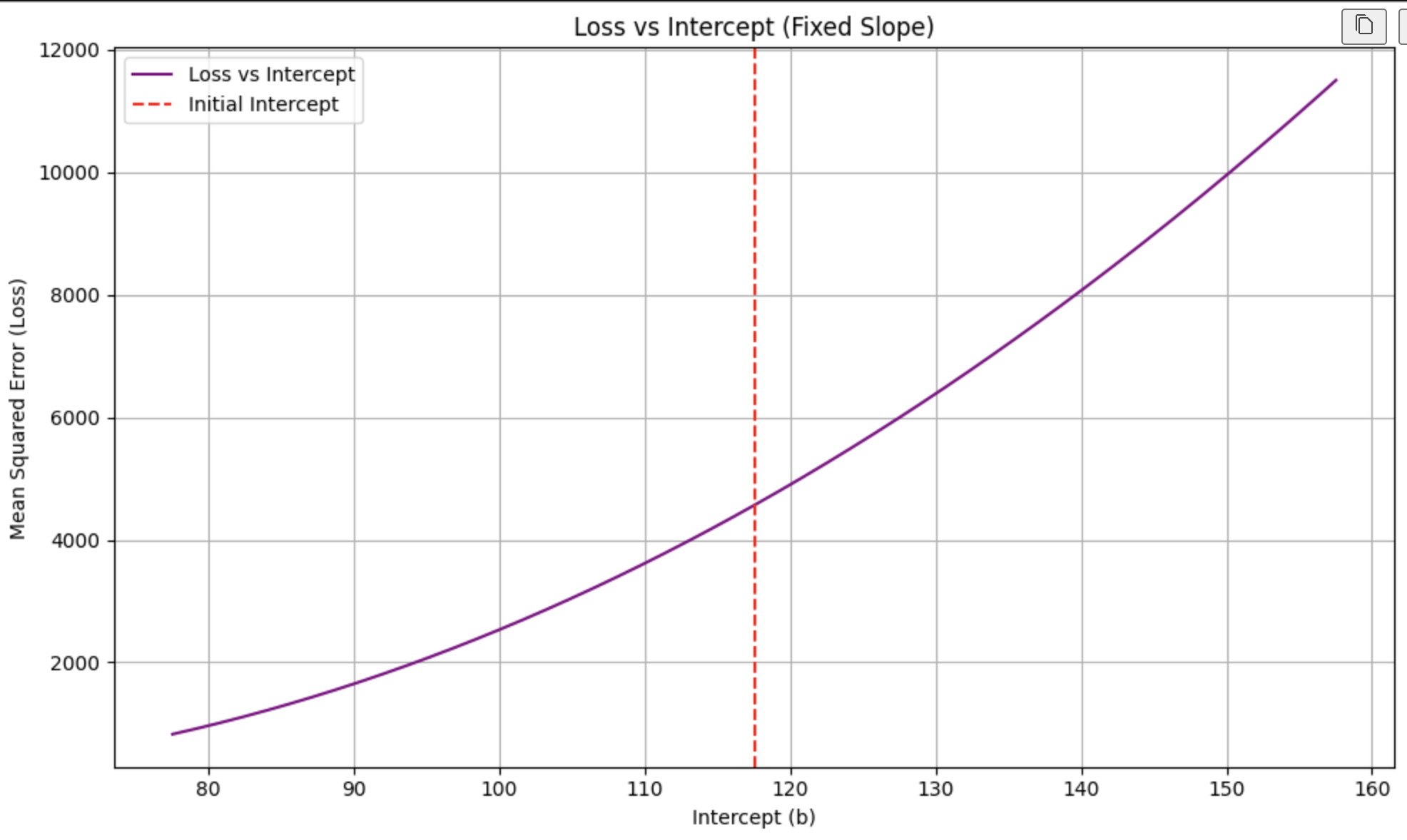
Gradient Descent
How to find the minimum value of the loss? It is the point where the slope of the function the closest to zero. How do we calculate slope in math? Derivative.
Gradient Descent is an optimization algorithm. It starts from a random point and takes steps in the direction that reduces the error, using the derivative (slope) to guide the way. As we get closer to the minimum error, our steps get smaller—just like climbing down a hill and slowing as you approach the bottom.
Step size = Slope * Learning Rate New Parameter = Old Parameter - Step Size
P.S.: Picking the optimal Learning Rate is also crucial but I'll explain it later on.
When you have two or more derivatives of the same function, they are called the Gradient. In our example slope and intercepts are Gradients and we find the optimal values of them to predict heights accurately. Regardless of which loss functions you use or how many parameters you have, Gradient Descent works the same way. More parameters, more derivatives.
We do these calculations at least a couple of tens of times hopefully to find the optimal values and that's where machines come to help us. It would have taken days to calculate these hundreds of derivatives by hand but thanks to our GPUs it takes only a few seconds.
The Algorithm Steps
Here are the steps you should follow:
- Step 1: Take the derivative of the loss function for each parameter in it.
- Step 2: Pick random values for the parameters.
- Step 3: Plug the parameter values into the derivatives.
- Step 4: Calculate step sizes.
- Step 5: Calculate new parameters.
Go back to step 3 and repeat until the step size is very small, or you reach the maximum number of steps.
Conclusion
With this foundation, you now understand the heart of how machines learn from data. Next, we can explore how this scales to more complex models and huge datasets!